2.5.矩形を紙面上で動かす
サイト内検索
マウスドラッグで自由に移動
自由な位置に移動するには、矩形素材を選択してから、マウスで移動したい位置までドラッグします。ドラッグ中の矩形枠線の上が、置きたい段に入るようやや下にするのがコツ。左右は、ドラッグした通りの位置になります。
💡
あえて段間に移動(段間を天位置に)したい場合は、ドラッグの点線が段間に入るようにします。
天地左右どこかの端に移動する場合は、紙面からはみ出す位置までドラッグしても大丈夫です(その方が確実に端に置けます)。
矢印キーで移動
素材を選択して、矢印キー(←→↑↓)で移動することも出来ます。段・行単位で移動
素材を選択して矢印キーを押すと、天地は１段、左右は１行分移動します。
↓
矢印キーは連続して押下することが出来ます。
→4回
文字目単位で上下に移動
Altキーを押しながら ↑↓ (横組なら←→) 押下で文字単位で移動します。段方向のみです。
↓6回
0.5文字等の刻みで移動
CtrlとAltキーを同時に押しながら 矢印キー押下で移動します。行方向は、0.5文字および0.5行間ごとに移動します。
段方向は、0.5文字および0.5段間ごとに移動します。(段間が１文字以上ある場合、0.5文字と0.5段間の両方の刻みで動きます)
詳細は2.11.任意のサイズと位置も参照してください。
１ピクセル単位で移動
Ctrlキーを押しながら、矢印キー押下で上下左右に１ピクセルずつ移動します。画面上のピクセル単位で動くので、紙面表示が拡大されているほど細かく動かせます。
詳細は2.11.任意のサイズと位置も参照してください。
他素材を押しながら移動
矢印キーによる移動では、移動方向にある素材も同時に動かせます。下図は、見出しの右側の罫線のみを選択して←キーを押した例。
←4回
移動と強制移動
上図の状態で、さらに←キーを押すと、以下のような確認ダイアログで出ます。
普通のマウスドラッグでは、移動先に別の矩形や記事があった場合、移動できません。
一方、矢印キーや、下で説明する右ドラッグでは、移動先に他の矩形や記事があると、矩形に押し出されるように一緒に移動します。
このように、他の素材を引き連れて移動することを本ソフトでは「強制移動」と呼んでいます。
[キャンセル]で取り消せます。
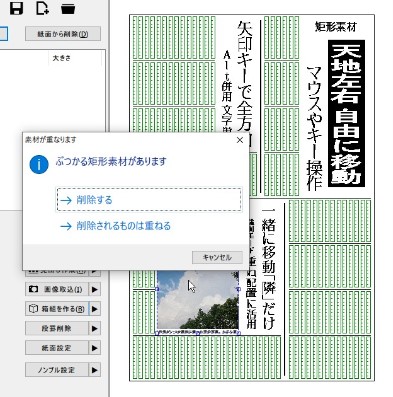
「重ね」か「削除」を選んだ場合は、以下のようになります。
｢重ね｣後
｢削除｣後
強制移動は"玉突き"しない
「押された矩形」がさらに別の矩形に当たった場合、その別の矩形までは動かさず、
「押し出された矩形」を削除するか、あるいは重ねて配置するか、選択できるダイアログが出ます(ここで移動のキャンセルも可能)。
「押された矩形」が紙面の端に当たった場合も同様です。
なお、矩形の「重ね配置」をするには、この特性を利用します。
複数素材をまとめて移動
複数選択して矢印キーを押します。 直接くっついていない矩形素材等もまとめて動かせます。
↑
⚠️
複数選択の場合、移動先に別素材があると重ねや削除は出来ず、移動しません。
また0.5刻みの移動はできません。
右ドラッグで移動
素材を選択して、マウスの右ボタンを押したままドラッグすると、矢印キーと同じく強制移動が出来ます。矢印キーと異なり、一度に複数の段や行を移動可能で、移動分量をリアルタイムで見ながら操作することが出来ます。
(アンドゥ・リドゥが１回で済むのも利点です)。
段・行単位で移動
矩形素材を選択して、右ドラッグします。最初に天地方向に動かすと天地に、左右方向だと行単位での強制移動になります。
[左に●行強制移動]など移動量がリアルタイムで表示されます。
文字目単位で上下に移動
Altキーを押しながら右ドラッグでマウスを上下方向に動かします。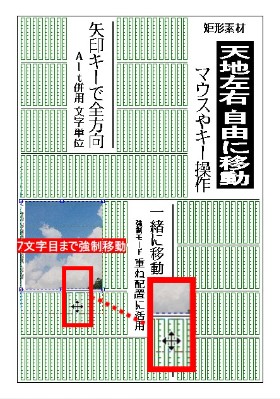
⚠️
移動時にカーソルが移動表示に当たると、うまく移動できない不具合があるので、矩形の上か下をドラッグしてください。
左右に動かした場合は、単に右ドラッグしたのと同じ結果になります。
右ドラッグの場合、複数素材をまとめての移動は出来ません。
右クリックメニューから移動
矩形素材を右クリックして、メニューから移動することも出来ます。現在、右クリックメニューの[移動]は強制移動です。
⚠️
移動の右クリックメニューについては、今後、仕様が追加・変更される可能性があります。
強制移動と記事の移動
強制移動の場合、矩形や記事が押し出されるように動きますが、記事に限っては"逆方向"でも動くようになっています。下図のような状態で見出しを右に１行強制移動した場合、右の罫線はもちろん、左側の記事も流し直されています。
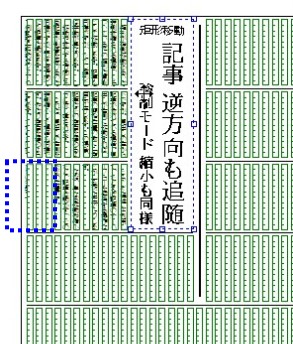
強制移動に伴う記事の再配置については、記事の畳みの有無やオーバーフローによって結果が異なります。
詳細については、4.2.移動･拡縮で記事動かす/4.3.天地の移動・拡縮と記事で解説します。